Недостатки NHDP

NHDP открывает соединения по первому полученному HELLO сообщению и закрываем по тайм-ауту. Недостатки:

• Ненадежность (низкая вероятность успешной передачи)
  • например получили только 1/3 от hello сообщений
  • не удовлетворяет требованию к доле досставленных пакетов из-за ограничения на число попыток передачи
  • высокое потребления канальных ресурсов из-за большого числа повторов передачи
  • хочется накладывать требования надежности
• Нестабильность (большая флуктуация состояния соединения)
  • постоянное изменения состояний узлов после новых сообщений
  • возможные ошибки маршрутизации (что-то вроде счетчика до бесконечности, следствие — циклы)

Возможное исправление:

Увеличение объема статистических данных на основании которого принимается решение об открытии соединения

• например наблюдать за параметрами hello сообщений (например уровень сигнала)
  • это трудно, тк протокол работает на уровне приложений, нужны драйверы и все такое
  • => нужны другие методы

Критерий надежности

Пусть задана некоторая вероятность = $p_0​$

Пусть вероятность успешной доставки = $p​$

Если $p>p_0$ то нужно close, если $p<p_0$ то нужно Symmetric

Критерий стабильности

Состояние то симметричное то не симметричное

$T_s​$ — среднее время жизни линка (логического соединения (когда соединение симметрично))

$T_N​$ — среднее время нахождения в Not Sym.

$g=\frac{1}{T_S+T_N}$ — link fluctuation (колебания)

$T_{update}$ — интервал обновления топологии (характерный период рассылки сетевой информации)

Сам критерий:

$\forall p => \frac{1}{g(p)} >> 2T_{update}$

Критерий оперативности

Важно, чтобы $T_{delay}$ (задержка до установки логического соединения) было много меньше $T_{link}$ (время физического соединения)

$T{delay} << T_{link}​$

Математическая модель

Говорим, что если хотя бы один из критериев не выполняется — у протокола маршрутизации большие проблемы.

Нужно построить математическую модель протокола, чтобы вычислять все эти значения.

Необходимо определить:

$\pi_{s}$ — вероятность того, что соединение симметрично

$T_{S}​$ — среднее время когда соединение симметрично

$T_{N}$ — среднее время когда соединение несимметрично

Упрощаем протокол, с точки зрения модели

Новая диаграмма состояний: (точнее правила перехода)

Важно обратить внимание на состояния $O=S+U$ и $N=U+C$

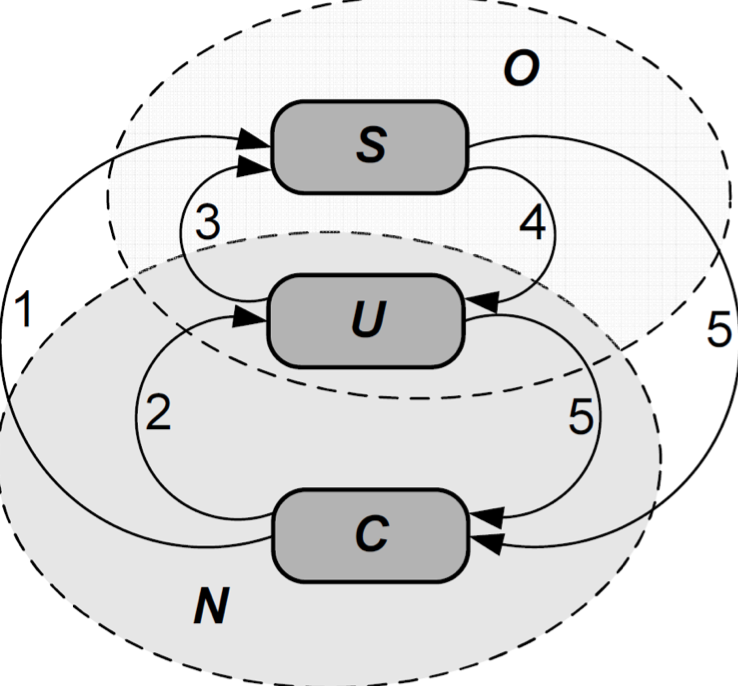
• Переходы из C в U и из C в S происходит, когда узел получает $r$ HELLO подряд от соседа [мб что-то улучшит, дополнительная степень свободы]

(Считаем, что HELLO генерируется строго периодично)

• Переход в C, когда потеряли $s​$ HELLO подряд. [тупо упрощаем модель]

Критерий Вальда — link

Сумма случайного числа одинаково-распределенных независимых случайных величин

Тождество Вальда

$E(\sum_{i-1}^{N}X_i) = E(N)E(X)​$

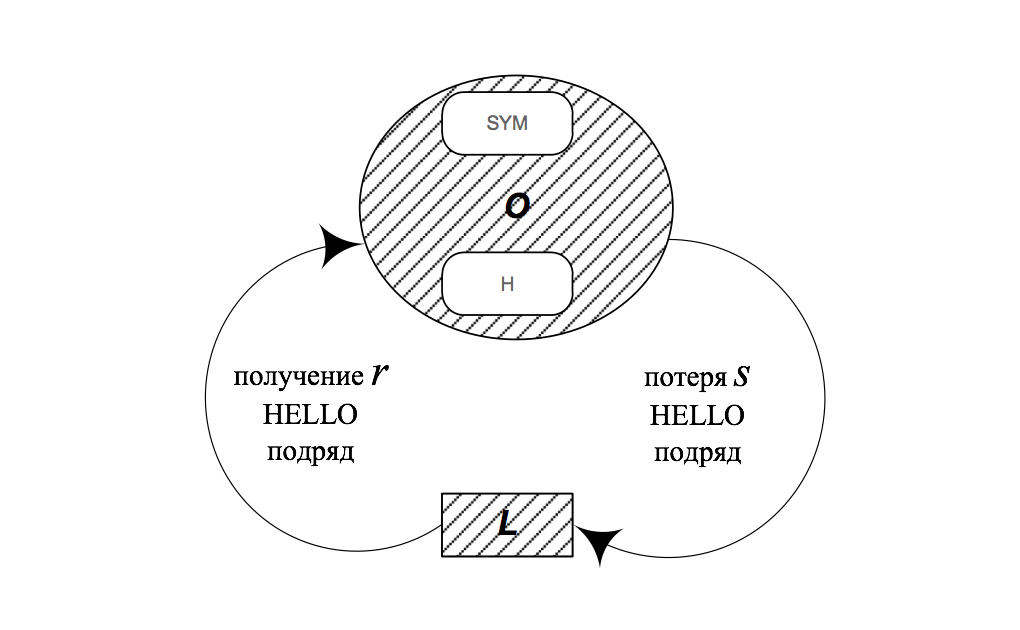
Определение вероятности нахождения в O(C)

Процесс $J_{oc}(t)$ перехода медлу состояними O и C является On-Off процессом

($<X>​$ — средняя длительность состояния X)

$\pi_{0}=\frac{<T_o>}{<T_o>+<T_c>}$

Определение средних длительностей состояний O,C

ДЗ 1

$<T_o>=\frac{1-(1-p)^s}{p(1-p)^s}​$

$<T_С>=\frac{1-p^r}{p^r(1-p)}$

($p$ вероятность единицы)

(выводится через формулу Вальда)

1#0001#1#01#01#0000000# (1 получили Hello, 0 потеряли)

Цикл продолжается до первой единицы или до s нулей.

Вероятность того, что длина цикла = s: $(1-p)​$

Какова средняя длина цикла?

Каково среднее число циклов?

Короче нужно ответить на эти вопросы и вывести формулы выше

Определение вероятности нахождения в состоянии S

Доказать утверждение

ДЗ 2

$\pi_{s}=\pi_o^2$

Подсказка: Состояние симметричное с точки зрения узла X, если оно открыто с точки зрения узла X и в последнем принятом HELLO от узла Y оно было указано как открытое

Доказать утверждение

ДЗ 3

$<T_S> \approx \frac{<T_o>}{2}$ (средняя длительность пересечений — смотреть картинку)

Подсказка:

• Важно знать, что отрезки одинаково распределены
• Считать, что нам известно распределение длины отрезка, оно вконце сократится
• Это классическая задача из тервера

ДЗ 4

Найти $T_{N}$ среднее вреся в нахождение $C+U$

Итого: 4 ДЗ

ДЗ 5*

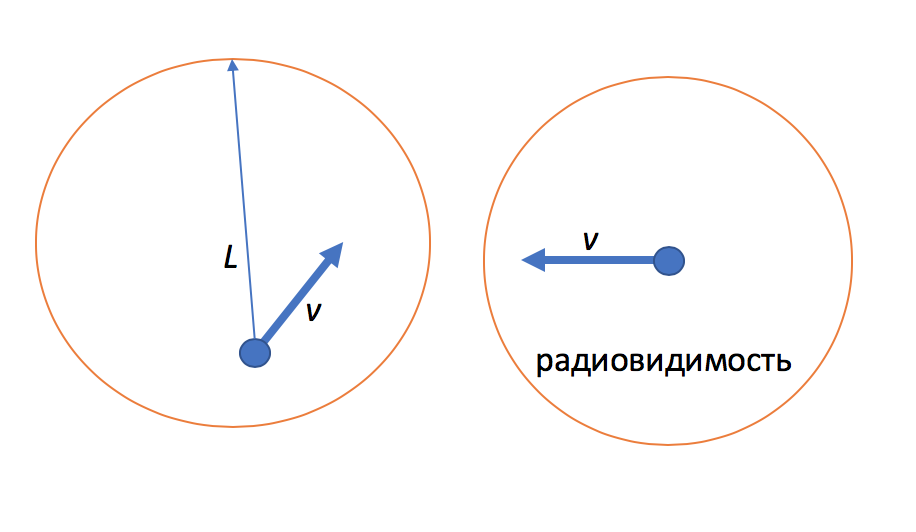
• 5-е дз со * (Среднее время жизни физического соединения)

$<T_{link}> = \frac{\pi^2*L}{8v}​$ среднее время движущихся объектов в зоне слышимости

Настройка параметров

Тут что-то говорится про выбор r, s и влияение на разные критерии, проще смотреть слайд.

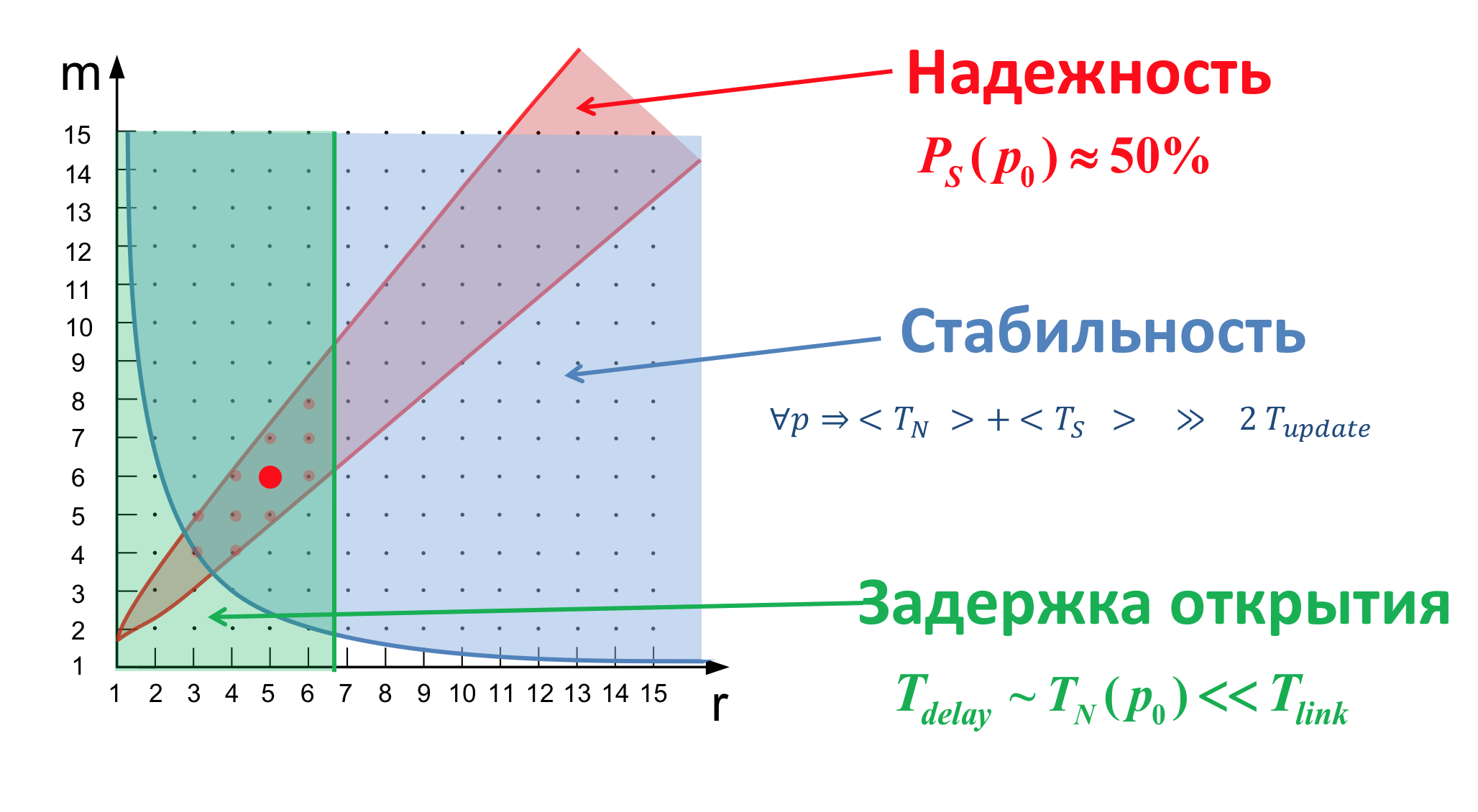
Что такое здесь $m$ — неясно (видимо $s$)